• 温故而知新，可以为师矣。发现有时候学的知识久了就容易忘，脑子一瞬间想不起来，加上学的东西越多越杂，一些基础的知识就会在恍惚间忘掉，这篇笔记主要记录一下学习神经网络的一些基础知识点，包括神经网络的前向传播模型推理和反向传播参数更新的原理和一些细节，以及采用numpy“手搓”一个BP神经网络进行一个实战演示。

神经网络

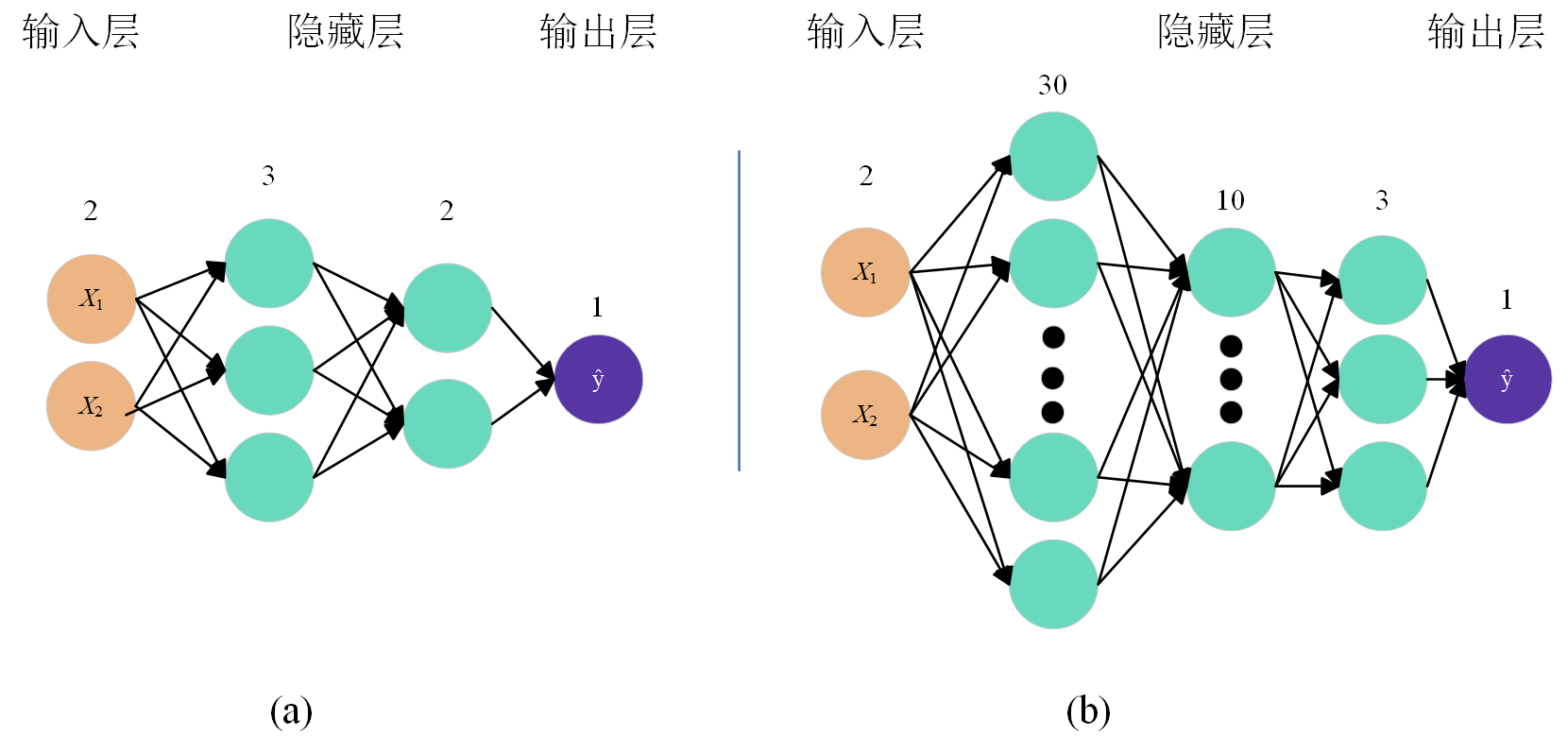
  • 神经网络的一些深刻概念和定义这里不再详细介绍，主要简单讲解一下的它的结构组成，神经网络由输入层、隐藏层和输出层构成，层内有神经元。而此神经元就是构建输入端与输出端复杂映射关系的关键，每个神经元就是一个数学公式 $$y=wx+b$$ ，层与层之间通过神经元连接从而构造输入数据（特征）之间的复杂联系。输入层和输出层一般都是单层，且其神经元个数一般也会由任务固定定义了，而隐藏层的层数和每层隐藏层内的神经元个数则是由学者根据具体工况设置，工况欲复杂其隐藏层数及神经元个数一般就会增加，但隐藏层的层数和神经元个数都是在学者反复训练、修改、对比后确定的，这个过程也就是常说的“神经网络模型结构超参数的优化选择”。下图1展示了两种不同的结构的神经网络模型。
图1
  • 上式是构成神经网络中神经元的核心运算，式中：y是神经元的输出值，x是神经元的输入值，w和b分别是神经元的权重(weight)和偏置(bias)，也就是神经网络的参数，神经网络学习的过程就是调整这两个值。

前向传播

  • 前向传播是指将输入数据通过神经网络层之间的神经元，逐层计算推理并传递到输出层的过程。就以图1中(a)神经网络进行简单讲解。(a)网络采用单层2神经元的输入层，两层隐藏层单元数分别为5和3，单层1个神经元的输出层搭建。输入层有两个神经元表明输入的数据特征为2，第一隐藏层的神经元为3，第二隐藏层的神经元为2，表明神经网络对输入特征先进行一个升维后再进行一个降维，最后由输出层的1个神经元输出单值结果。

  • 隐藏层在神经网络起到一个特征变换的作用，包括特征升维和降维。特征升维是将原始特征维度映射到更高维度空间，以增加特征丰富度，捕捉更复杂的模式。特征降维则是将原始特征维度映射到低维度空间，同时尽可能保留数据中重要信息，以降低计算成本、去除冗余信息。隐藏层也是通过非线性激活函数对层输入数据进行非线性变换，将输入特征引入非线性特征空间的关键。下图2展示了神经网络前向传播的推理过程。

图2

损失计算

  • 损失计算是指衡量模型预测值与真实值之间差异的过程，对于每一个输入样本，模型都会产生一个预测输出（注：这里的“一个”指的是样本数不是特征数）。通过将这个预测输出值与该样本的真实值进行比较，计算出一个数值，这个数值就是该样本的损失值也称为误差。
  • 损失函数一般可分为两个大类：回归与分类。回归的损失函数一般常用有均方差损失函数(MSE)，平均绝对误差损失函数(MAE)等，分类的损失函数就是交叉熵，二元交叉熵损失函数(Binary Cross-Entropy)和多分类交叉熵损失函数(Categorical Cross-Entropy)。这次搭建一个简单的回归网络就用MSE损失函数。

$$ MSE=\frac{1}{n}\sum_{n}^{i=1}\left ( \hat{y_{i}} -y_{i} \right )^{2} $$

  • 式中：ŷi为第i个样本的预测值，yi为第i个样本的真实值，n为样本数。

反向传播

  • 反向传播是神经网络训练的关键技术，它用于计算损失函数关于网络中各个参数（权重和偏置）的梯度（偏导数）。梯度计算过程利用了微积分中的链式法则，反向逐层计算每个参数的偏导数，这些梯度随后被优化器用来更新参数（参数的更新也必须遵守反向逐层参数更新），从而减小损失函数，提高模型的性能。下图3展示了神经网络反向传播的过程。
图3

BP神经网络的搭建

  • 通过前面的简单回归神经网络的已经明白了神经网络的前向传播和反向传播以及神经网络中参数的迭代更新，现在搭建图1(b)的BP神经网络模型，前两个隐藏层采用Sigmoid激活函数，后一层隐藏层采用ReLu激活函数。搭建步骤通过代码注释逐步讲解。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
import numpy as np


class RegressionNet:
    """
    The BP-Net was created for 1 input layer, 3 hidden layers and 1 output layer
    input_layer: 3 units(features)
    1th hidden layer: 30 units
    2th hidden layer: 10 units
    3th hidden layer: 3 units
    output_layer: 1 units
    """
    def __init__(self):
        """
        通过numpy.random.randn生成正态分布参数权重和偏置初始值，并设置学习率lr为0.01
        """
        self.lr = 0.01
        self.w1 = np.random.randn(30, 3)
        self.b1 = np.random.randn(30, 1)
        self.w2 = np.random.randn(10, 30)
        self.b2 = np.random.randn(10, 1)
        self.w3 = np.random.randn(3, 10)
        self.b3 = np.random.randn(3, 1)
        self.w4 = np.random.randn(1, 3)
        self.b4 = np.random.randn(1, 1)

    # ReLu激活函数
    def relu(self, x):
        return np.where(x > 0, x, 0)

    # ReLu激活函数的求导
    def relu_derivative(self, x):
        return np.where(x > 0, 1, 0)

    # Sigmoid激活函数
    def sigmoid(self, x):
        return 1/(1+np.exp(-x))

    # Sigmoid激活函数求导
    def sigmoid_derivative(self, x):
        return self.sigmoid(x)*(1-self.sigmoid(x))

    # MSE均方差损失函数
    def mse(self, y, y_hat):
        return np.mean((y-y_hat)**2)

    # 前向传播
    def forward(self, x):
        assert x.shape[0] == self.w1.shape[1]
        self.z1 = self.w1@x + self.b1
        self.a1 = self.sigmoid(self.z1)
        self.z2 = self.w2@self.a1 + self.b2
        self.a2 = self.sigmoid(self.z2)
        self.z3 = self.w3@self.a2 + self.b3
        self.a3 = self.relu(self.z3)
        self.y_hat = self.w4@self.a3 + self.b4

        return self.y_hat

    # 反向传播
    def backward(self, x, y, y_hat):
        # 链式法则求导
        m = x.shape[1]
        dy_hat = -2*(y-y_hat)/m
        dw4 = dy_hat@self.a3.T
        db4 = np.mean(dy_hat, axis=1, keepdims=True)  # 这里的mean的操作是对训练样本进行均值处理，下同
        da3 = self.w4.T@dy_hat
        dz3 = da3*self.relu_derivative(self.z3)
        dw3 = dz3@self.a2.T
        db3 = np.mean(dz3, axis=1, keepdims=True)
        da2 = self.w3.T@dz3
        dz2 = da2*self.sigmoid_derivative(self.z2)
        dw2 = dz2@self.a1.T
        db2 = np.mean(dz2, axis=1, keepdims=True)
        da1 = self.w2.T@dz2
        dz1 = da1*self.sigmoid_derivative(self.z1)
        dw1 = dz1@x.T
        db1 = np.mean(dz1, axis=1, keepdims=True)

        # 参数更新
        self.w4 = self.w4 - self.lr*dw4
        self.b4 = self.b4 - self.lr*db4
        self.w3 = self.w3 - self.lr*dw3
        self.b3 = self.b3 - self.lr*db3
        self.w2 = self.w2 - self.lr*dw2
        self.b2 = self.b2 - self.lr*db2
        self.w1 = self.w1 - self.lr*dw1
        self.b1 = self.b1 - self.lr*db1

    # 网络训练
    def train(self, x, y):
        y_hat = self.forward(x)
        loss = self.mse(y, y_hat)
        # 进行反向传播
        self.backward(x, y, y_hat)
        return loss

    # 网络测试
    def test(self, x):
        y_hat = self.forward(x)
        return y_hat